Berbagi ILmu: Himpunan (Matematika)

Himpunan (matematika)

Referensi

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas

Dalam matematika, himpunan adalah segala koleksi benda-benda tertentu yang dianggap sebagai satu kesatuan. Walaupun hal ini merupakan ide yang sederhana, tidak salah jika himpunan merupakan salah satu konsep penting dan mendasar dalam matematika modern, dan karenanya, studi mengenai struktur kemungkinan himpunan dan teori himpunan, sangatlah berguna.

Irisan dari dua himpunan yang dinyatakan dengan diagram Venn

Teori himpunan, yang baru diciptakan pada akhir abad ke-19, sekarang merupakan bagian yang tersebar dalam pendidikan matematika yang mulai diperkenalkan bahkan sejak tingkat sekolah dasar. Teori ini merupakan bahasa untuk menjelaskan matematika modern. Teori himpunan dapat dianggap sebagai dasar yang membangun hampir semua aspek dari matematika dan merupakan sumber dari mana semua matematika diturunkan.

Notasi Himpunan

Biasanya, nama himpunan ditulis menggunakan huruf besar, misalnya S, A, atau B, sementara elemen himpunan ditulis menggunakan huruf kecil (a, c, z). Cara penulisan ini adalah yang umum dipakai, tetapi tidak membatasi bahwa setiap himpunan harus ditulis dengan cara seperti itu. Tabel di bawah ini menunjukkan format penulisan himpunan yang umum dipakai.

	Notasi	Contoh
Himpunan	Huruf besar	S
Elemen himpunan	Huruf kecil (jika merupakan huruf)	a
Kelas	Huruf tulisan tangan	$\mathbb{C}$

Himpunan-himpunan bilangan yang cukup dikenal, seperti bilangan kompleks, riil, bulat, dan sebagainya, menggunakan notasi yang khusus.

Bilangan

Asli

Bulat

Rasional

Riil

Kompleks

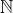
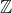
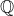
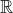
Notasi $\mathbb{N}$ $\mathbb{Z}$ $\mathbb{Q}$ $\mathbb{R}$ $\mathbb{C}$

Simbol

Arti

              $\varnothing$                                     Himpunan kosong
              $\cup$                                     operasi gabungan dua himpunan
              $\cap$    operasi irisan dua himpunan
             $A^{c}$ Komplement
          $P(A)$    Himpunan kuasa

Himpunan dapat didefinisikan dengan dua cara, yaitu:

Enumerasi, yaitu mendaftarkan semua anggota himpunan. Jika terlampau banyak tetapi mengikuti pola tertentu, dapat digunakan elipsis (...).

B = $\left \{ Apel, Mangga, Jeruk, Pisang \right \}$

A = $\left \{ a,b,c,d,.....y,z\right \}$

$\mathbb{N}= \left \{1,2,3,4.... \right \}$

Pembangun himpunan, tidak dengan mendaftar, tetapi dengan mendeskripsikan sifat-sifat yang harus dipenuhi oleh setiap elemen himpuan tersebut.

O = { u | u adalah bilangan ganjil }

E = {x | x ϵ Z ˄ (x mod 2 =0)}

P = { p| p adalah orang yang pernah menjabat sebagai preesiden RI }

Notasi pembangun himpunan dapat menimbulkan berbagai paradoks, contohnya adalah himpunan berikut:

A = { x| x ϵ A }

Himpunan A tidak mungkin ada, karena jika A ada, berarti harus mengandung anggota yang bukan merupakan anggotanya. Namun jika bukan anggotanya, lalu bagaimana mungkin A bisa mengandung anggota tersebut.

Himpunan kosong

Himpunan {apel, jeruk, mangga, pisang} memiliki anggota-anggota apel, jeruk, mangga, dan pisang. Himpunan lain, semisal {5, 6} memiliki dua anggota, yaitu bilangan 5 dan 6. Kita boleh mendefinisikan sebuah himpunan yang tidak memiliki anggota apa pun. Himpunan ini disebut sebagai himpunan kosong.

Himpunan kosong tidak memiliki anggota apa pun, ditulis sebagai:

ᴓ = {}

Relasi antar himpunan

Subhimpunan

Dari suatu himpunan, misalnya A = {apel, jeruk, mangga, pisang}, dapat dibuat himpunan-himpunan lain yang elemen-elemennya adalah diambil dari himpunan tersebut.

{apel, jeruk}
{jeruk, pisang}
{apel, mangga, pisang}

Ketiga himpunan di atas memiliki sifat umum, yaitu setiap anggota himpunan itu adalah juga anggota himpunan A. Himpunan-himpunan ini disebut sebagai subhimpunan atau himpunan bagian dari A. Jadi dapat dirumuskan:

B adalah himpunan bagian dari A jika setiap elemen B juga terdapat dalam A.

B ⊆ A ≡ ∀_x x ϵ B →x ϵ A

Kalimat di atas tetap benar untuk B himpunan kosong. Maka $\varnothing$ juga subhimpunan dari A.

Untuk sembarang himpunan A,

∅ ⊆ A

Definisi di atas juga mencakup kemungkinan bahwa himpunan bagian dari A adalah A sendiri.

Untuk sembarang himpunan A,

A ⊆ A

Istilah subhimpunan dari A biasanya berarti mencakup A sebagai subhimpunannya sendiri. Kadang-kadang istilah ini juga dipakai untuk menyebut himpunan bagian dari A, tetapi bukan A sendiri. Pengertian mana yang digunakan biasanya jelas dari konteksnya.

Subhimpunan sejati dari A menunjuk pada subhimpunan dari A, tetapi tidak mencakup A sendiri.

B ⊂ A ≡ B ⊆ A ˄ B ≠ A

Superhimpunan

Kebalikan dari subhimpunan adalah superhimpunan, yaitu himpunan yang lebih besar yang mencakup himpunan tersebut.

A ⊇ B ≡ B ⊆ A

Kesamaan dua himpunan

Himpunan A dan B disebut sama, jika setiap anggota A adalah anggota B, dan sebaliknya, setiap anggota B adalah anggota A.

A = B ≡ ∀_x x ϵ A ↔ x ϵB

atau

A = B ≡ A ⊆ B ˄ B ⊆ A

Definisi di atas sangat berguna untuk membuktikan bahwa dua himpunan A dan B adalah sama. Pertama, buktikan dahulu A adalah subhimpunan B, kemudian buktikan bahwa B adalah subhimpunan A.

Himpunan Kuasa

Himpunan kuasa atau himpunan pangkat (power set) dari A adalah himpunan yang terdiri dari seluruh himpunan bagian dari A. Notasinya adalah P (A).

Jika A = {apel, jeruk, mangga, pisang}, maka P (A)

{ { },

{apel}, {jeruk}, {mangga}, {pisang},

{apel, jeruk}, {apel, mangga}, {apel, pisang},

{jeruk, mangga}, {jeruk, pisang}, {mangga, pisang},

{apel, jeruk, mangga}, {apel, jeruk, pisang}, {apel, mangga, pisang}, {jeruk, mangga, pisang},

{apel, jeruk, mangga, pisang} }

Banyaknya anggota yang terkandung dalam himpunan kuasa dari A adalah 2 pangkat banyaknya anggota A.

P(A)| = 2 ^|A|

Kelas

Suatu himpunan disebut sebagai kelas, atau keluarga himpunan jika himpunan tersebut terdiri dari himpunan-himpunan. Himpunan

A = {{a,b}, {c,d,e,f}, {a,c}, {,}}adalah sebuah keluarga himpunan. Perhatikan bahwa untuk sembarang himpunan A, maka himpunan kuasanya, P (A)adalah sebuah keluarga himpunan.

Contoh berikut, P= {{a,b},c}bukanlah sebuah kelas, karena mengandung elemen c yang bukan himpunan.

Kardinalitas

Kardinalitas dari sebuah himpunan dapat dimengerti sebagai ukuran banyaknya elemen yang dikandung oleh himpunan tersebut. Banyaknya elemen himpunan {apel,jeruk,mangga,pisang} adalah 4. Himpunan {p,q,r,s} juga memiliki elemen sejumlah 4. Berarti kedua himpunan tersebut ekivalen satu sama lain, atau dikatakan memiliki kardinalitas yang sama.

Dua buah himpunan A dan B memiliki kardinalitas yang sama, jika terdapat fungsi korespondensi satu-satu yang memetakan A pada B. Karena dengan mudah kita membuat fungsi

{(apel,p), (jeruk,q), (mangga,r), (pisang,s)} yang memetakan satu-satu dan kepada himpunan A ke B, maka kedua himpunan tersebut memiliki kardinalitas yang sama.

Himpunan Denumerabel

Jika sebuah himpunan ekivalen dengan himpunan N, yaitu himpunan bilangan asli, maka himpunan tersebut disebut denumerabel. Kardinalitas dari himpunan tersebut disebut sebagai kardinalitas a

Himpunan semua bilangan genap positif merupakan himpunan denumerabel, karena memiliki korespondensi satu-satu antara himpunan tersebut dengan himpunan bilangan asli, yang dinyatakan oleh 2n

A= {2, 4, 6, 8,...}

[Himpunan Berhingga

Jika sebuah himpunan memiliki kardinalitas yang kurang dari kardinalitas $\mathfrak{a}$ , maka himpunan tersebut adalah himpunan berhingga.

Himpunan Tercacah

Himpunan disebut tercacah jika himpunan tersebut adalah berhingga atau denumerabel.

Himpunan Non-Denumerabel

Himpunan yang tidak tercacah disebut himpunan non-denumerabel. Contoh dari himpunan ini adalah himpunan semua bilangan riil. Kardinalitas dari himpunan jenis ini disebut sebagai kardinalitas c

Pembuktian bahwa bilangan riil tidak denumerabel dapat menggunakan pembuktian diagonal.

Himpunan bilangan riil dalam interval (0,1) juga memiliki kardinalitas c karena terdapat korespondensi satu-satu dari himpunan tersebut dengan himpunan seluruh bilangan riil, yang salah satunya adalah

Fungsi Karakteristik

Fungsi karakteristik menunjukkan apakah sebuah elemen terdapat dalam sebuah himpunan atau tidak.

1, jika x ϵ A

X_A (x) =

0, jika x ϵ A

Jika

A = { apel, jeruk, mangga, pisang} maka:

χ_A(apel) = 1

χ_A(durian) = 0

χ_A(utara) = 0

χ_A(pisang) = 1

χ_A(singa) = 0

Terdapat korespondensi satu-satu antara himpunan kuasa

P(s)dengan himpunan dari semua fungsi karakteristik dari S. Hal ini mengakibatkan kita dapat menuliskan himpunan sebagai barisan bilangan 0 dan 1, yang menyatakan ada tidaknya sebuah elemen dalam himpunan tersebut.

Representasi Biner

Jika konteks pembicaraan adalah pada sebuah himpunan semesta S, maka setiap himpunan bagian dari S bisa dituliskan dalam barisan angka 0 dan 1, atau disebut juga bentuk biner. Bilangan biner menggunakan angka 1 dan 0 pada setiap digitnya. Setiap posisi bit dikaitkan dengan masing-masing elemen S, sehingga nilai 1 menunjukkan bahwa elemen tersebut ada, dan nilai 0 menunjukkan bahwa elemen tersebut tidak ada. Dengan kata lain, masing-masing bit merupakan fungsi karakteristik dari himpunan tersebut. Sebagai contoh, jika himpunan S = {a, b, c, d, e, f, g}, A = {a, c, e, f}, dan B = {b, c, d, f}, maka:

Himpunan Representasi Biner

---------------------------- -------------------

a b c d e f g

S = { a, b, c, d, e, f, g } --> 1 1 1 1 1 1 1

A = { a, c, e, f } --> 1 0 1 0 1 1 0

B = { b, c, d, f } --> 0 1 1 1 0 1 0

Cara menyatakan himpunan seperti ini sangat menguntungkan untuk melakukan operasi-operasi himpunan, seperti union, interseksi, dan komplemen, karena kita tinggal menggunakan operasi bit untuk melakukannya.

Operasi gabungan AᴜB setara dengan A or B
Operasi irisan A∩B setara dengan A and B
Operasi komplemen A^C setara dengan not

Representasi himpunan dalam bentuk biner dipakai oleh kompiler-kompiler Pascal dan juga Delphi.

Wikibooks memiliki buku bertajuk

Materi:Himpunan

Referensi

Lipschutz, S. Set Theory. McGraw-Hill
Delphi 5 Memory Management

Bacaan lanjutan

Halmos, Paul R., Naive Set Theory, Princeton, N.J.: Van Nostrand (1960) ISBN 0-387-90092-6
Stoll, Robert R., Set Theory and Logic, Mineola, N.Y.: Dover Publications (1979) ISBN 0-486-63829-4

Diperoleh dari "http://id.wikipedia.org/wiki/Himpunan_(matematika)"

Kategori: Teori himpunan

Berbagi ILmu

Jumat, 21 Oktober 2011

Himpunan (Matematika)

Tidak ada komentar:

Posting Komentar

Materi Populer

Cari Blog Ini

Label