by
Taufiq Hidayat
Tulisan-tulisan di kategori Logika Matematika ini hanya ditujukan
untuk mereka yang sedang belajar hal-hal dasar tentang Logika Matematika. Akan
jarang ditemui hal-hal yang baru di sini. Semoga bermanfaat.
Saat mengajar kuliah Pemrograman Non Prosedural (terutama bagian
Pemrograman Logika), saya banyak menemui mahasiswa yang belum memahami kegunaan
logika matematika, terutama dalam kehidupan sehari-hari. Padahal tujuan utama
semua ilmu adalah membantu kehidupan manusia. Demikian juga dengan logika
matematika. Salah satu manfaatnya adalah membantu membuat (menarik) kesimpulan
yang benar. Tulisan ini akan membahas tentang teknik penarikan kesimpulan
dasar, yaitu Modus Ponens dan Modus Tollens.
Agar cakupannya tidak meluas, jenis logika yang saya pakai di tulisan ini
adalah logika proposisi (propositional logic). Dalam logika proposisi,
sebuah kalimat dinyatakan dengan sebuah simbol (yang mungkin berindeks).
Contoh 1:
p : saya makan di kelasq : saya minum di kelas
p 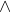 q : saya makan di kelas dan saya minum di kelas
(disingkat: saya makan dan minum di kelas)
q : saya makan di kelas dan saya minum di kelas
(disingkat: saya makan dan minum di kelas)
p p
~ p : saya tidak makan di kelas.
Modus Ponens dan Modus Tollens sebenarnya adalah teknik penarikan
kesimpulan dari logika manusia juga. Di Logika Matematika, kedua teknik
penarikan kesimpulan tersebut dinyatakan dengan:
Modus Ponens
p
p
———
Kesimpulan: q
———
Kesimpulan: q
Modus Tollens
p
¬ q
———
Kesimpulan: ¬ p
———
Kesimpulan: ¬ p
Arti Modus Ponens adalah “jika diketahui p  q dan p, maka bisa ditarik kesimpulan q“. Sedangkan Modus
Tollens berarti “jika diketahu p
q dan p, maka bisa ditarik kesimpulan q“. Sedangkan Modus
Tollens berarti “jika diketahu p  q dan ¬q, maka bisa ditarik kesimpulan ¬p“.
q dan ¬q, maka bisa ditarik kesimpulan ¬p“.
Contoh 2:
Diketahui cerita sederhana berikut: Jika saya makan di kelas maka saya
minum di kelas. Saya makan di kelas. Apakah saya minum di kelas?
Solusi:
Menggunakan Contoh 1 di atas, kita memperoleh kalimat matematika:
p Menggunakan Contoh 1 di atas, kita memperoleh kalimat matematika:
p
Menggunakan Modus Ponens, maka kita bisa menarik kesimpulan q, yang
artinya saya minum di kelas.
—————- []
Contoh 3:
Diketahui cerita sederhana berikut: Jika saya makan di kelas maka saya
minum di kelas. Saya tidak minum di kelas. Apakah saya makan di kelas?
Solusi:
Menggunakan Contoh 1 di atas, kita memperoleh kalimat matematika:
Menggunakan Contoh 1 di atas, kita memperoleh kalimat matematika:
p  q
q
¬q
¬q
Menggunakan Modus Tollens, maka kita bisa menarik kesimpulan ¬p,
yang artinya saya tidak makan di kelas.
—————- []
Contoh 4:
Diketahui cerita sederhana berikut: Jika saya makan di kelas maka saya
minum di kelas. Jika saya minum di kelas maka ruangan kelas menjadi
kotor. Saya makan di kelas. Apakah ruangan kotor?
Solusi:
Misalkan:
p : saya makan di kelas
q : saya minum di kelas
r : ruangan kelas menjadi kotor
q : saya minum di kelas
r : ruangan kelas menjadi kotor
maka, cerita sederhana tersebut dapat dinyatakan dengan
1: p  q
q
2: q r
r
3: p
2: q
3: p
Menggunakan Modus Ponens untuk kalimat 1 dan kalimat 3, maka kita bisa
menarik kesimpulan q, yang artinya saya minum di kelas.
Kalimat-kalimat matematikanya bisa kita ubah menjadi:
1: p  q
q
2: q r
r
3: p
4: q
2: q
3: p
4: q
Dengan menggunakan Modus Ponens untuk kalimat 2 dan 4, kita memperoleh
kesimpulan r, yang artinya ruangan kelas menjadi kotor.
—————- []
Contoh 5:
Diketahui cerita sederhana berikut: Jika saya makan maka saya tidak
belajar. Jika televisi sedang mati maka saya belajar. Saat ini, televisi sedang
mati. Apakah saya sedang makan?
Solusi:
Misalkan:
p : saya makan
q : saya belajar
r : televisi mati
q : saya belajar
r : televisi mati
maka, cerita sederhana tersebut dapat dinyatakan dengan
1: p  ¬q
¬q
2: r q
q
3: r
2: r
3: r
Kesimpulan dengan Modus Ponens untuk kalimat 2 dan kalimat 3: q.
Kalimat matematika diubah menjadi:
Kalimat matematika diubah menjadi:
1: p  ¬q
¬q
2: r q
q
3: r
4: q
2: r
3: r
4: q
Dengan menggunakan Modus Tollens untuk kalimat 1 dan kalimat 4, kita
peroleh kesimpulan ¬p, yang artinya saya tidak makan.
—————- []
Cerita di contoh-contoh di atas adalah sederhana. Namun bukan berarti
contoh yang lebih kompleks tidak bisa diselesaikan dengan teknik ini. Berikut
adalah contoh dengan cerita yang lebih kompleks.
Contoh 6:
Diketahui cerita berikut: Pak Ali biasa ke kantor menggunakan mobil. Tentu
saja jika mobilnya tidak mengalami masalah. Kalau mobilnya punya masalah, dia
akan menggunakan angkutan umum. Biasanya dia mengetahui bahwa mobilnya punya
masalah saat mau berangkat, menyebabkan dia terlambat tiba di kantor. Tetapi
dia juga bisa terlambat meskipun naik mobil karena jalannya macet. Gara-gara
terlambat, dia tidak bisa menghabiskan kopinya, yang sudah disediakan di dapur
kantor. Pagi ini terlihat kopinya sudah habis. Pertanyaan:
a. Apakah mobil pak Ali bermasalah?
b. Apakah jalanan macet?
a. Apakah mobil pak Ali bermasalah?
b. Apakah jalanan macet?
Solusi:
Misalkan:
p : mobil Pak Ali bermasalah
q : Pak Ali ke kantor naik mobil
r : Pak Ali ke kantor naik angkutan umum
s : Pak Ali terlambat
t : Jalanan macet
u : Kopinya Pak Ali habis.
q : Pak Ali ke kantor naik mobil
r : Pak Ali ke kantor naik angkutan umum
s : Pak Ali terlambat
t : Jalanan macet
u : Kopinya Pak Ali habis.
maka, cerita tersebut dapat dinyatakan dengan
1: p  r
r
2: ¬p q
q
3: r s
s
4: q Λ t s
s
5: s ¬u
¬u
6: u
2: ¬p
3: r
4: q Λ t
5: s
6: u
Kesimpulan yang bisa diambil:
7: ¬s {Modus Tollens dari 5 dan 6}
8: ¬r {Modus Tollens dari 3 dan 7}
9: ¬p {Modus Tollens dari 1 dan 8}
8: ¬r {Modus Tollens dari 3 dan 7}
9: ¬p {Modus Tollens dari 1 dan 8}
Arti kalimat
9: mobil Pak Ali tidak bermasalah (Jawaban
untuk pertanyaan a).
Kesimpulan untuk menjawab pertanyaan b:
Kesimpulan untuk menjawab pertanyaan b:
10: q {Modus Ponens dari 2 dan 9}
11: ¬(q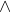 t) {Modus Tollens dari 4
dan 7}
t) {Modus Tollens dari 4
dan 7}
12: ¬q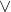 ¬t {Hukum de Morgan untuk
11}
¬t {Hukum de Morgan untuk
11}
13: q → ¬t {Ekuivalensi implikasi dengan 12}
14: ¬t {Modus Ponens dari 10 dan 13}
11: ¬(q
12: ¬q
13: q → ¬t {Ekuivalensi implikasi dengan 12}
14: ¬t {Modus Ponens dari 10 dan 13}
Kalimat 14
berarti Jalanan tidak macet (Jawaban untuk
pertanyaan b).
—————- []
Catatan
Tambahan:
Hukum de
Morgan:
¬(p 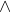 q) ≡ (¬p
q) ≡ (¬p 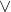 ¬q)
¬q)
¬(p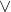 q) ≡ (¬p
q) ≡ (¬p 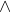 ¬q)
¬q)
¬(p
Ekuivalensi
implikasi:
(p  q) ≡ (¬p
q) ≡ (¬p 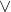 q)
q)
Gunakan prinsip inferensi untuk menurunkan -S dari hipotesa-hipotesa :
BalasHapus(S V Q) -> P
-A
P -> A
kl keak gt tuh ngerjainya gmana y kak ?
mhn bantuanya, mksih :D